
back to The Kabbalistic Tree of Life

This article is also available in PDF format
|
This diagram contains ten circles representing the Sephiroth (singular: Sephirah); that is, the "spheres," "numbers," or "emanations". The Sephiroth are the numbers 1 through 10 considered in their archetypal sense. Each Sephirah is an archetypal idea. Also, the Sephiroth represent emanations from God and describe the process of creation. In the material world, they represent the heavenly spheres according to the classical conception. The Tree of Life, or the Kabbalah, is a Kabbalistic a map of consciousness, a geometrical symbol of the complete universe, composed of ten spheres, called the Sephiroth, and 22 connecting paths. It is a diagrammatic representation of the thirty-two Paths of Wisdom, which relate to the number of times that the name of God was found in the Genesis. The Kabbalists understood that the mysteries of life couldn’t be proved and for that reason they developed, through the combination of many elements of religion and mathematics, the kabalistic paths whose aid of understanding is to know oneself and the laws and forces of the Universe. The micro and macrocosmic view of existence. According to the Kabbalistic teaching, the creation occurred because of a withdrawal of the Light of the Creator. God manifested the Sephirot which are a sequence of ten energy fields which keep us protected from the full intensity of His Light. Each Sephirah has distinctive qualities, properties and lessons to be absorbed and mastered. The ten Sephirot are the manifestation of states of consciousness, and they act as transformers as we work with them. |
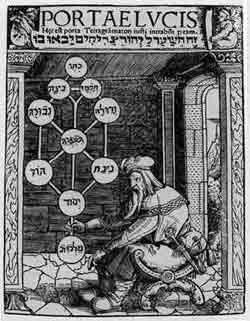
From an old manuscript of Paulus Richius.
|
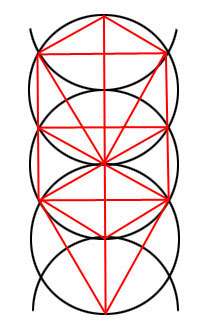
I always wondered why the Kabalistic Tree of Life has the shape it has. It has an unusual shape; how did the Cabalists decide to use such a shape? One day I discovered that it is drawn in interlocking circles. |
|
Why interlocking circles? Well, they are the product of a mathematical genesis. Let me explain. First there is the Nothing. The Ain, or Ain-Soph, the great limitless Nothingness of which nothing can be said. Then a point arises out of the Ain-Soph. God brings forth the immensity of eternal extension. With our limited human understanding we call this "non-existence". God withdraws himself from himself and creates an emptiness and a place for the Ain-Soph. The next thing is a circle. It encompasses the entire created emptiness. It is like the extension off the point. From this duality arises. There the point and the circle, the male and the female, the positive and the negative. |
|
Somewhere on the circle we determine a point, that will serve as the center of a new circle. With duality in existence we now can create a duplicate circle. The circle mirrors itself:
|
|
This simple act brings forth a lot of interesting things.
The Vesica Pisces:
The overlapping area is a "Vesica Pisces", a symbol used in early Christian days for Christ. The almost oval shape is also a universal symbol for the yoni, the female sexual organ used by many cultures for the Great Mother. It is well known in Eastern religions, but Mother Mary in the Catholic Church was also frequently depicted with the same symbol behind or around her. |
|
From one point, the center of the first circle, arises four points: the two centers of the two circles plus the two intersection points of the two circles. All four points can be connected to each other and produces the following result: |
|
From unity we went to duality to quaternity. The Four Elements are a quaternity as it is said that they are interrelated, they cannot exist without one another. They come forth out of unity and they dissolve into unity. The Four Elements are the foundation out of which the entire universe is built. The resulting diamond shape brings forth some interesting things: The
diamond shape is related to the number four and quaternity, but it brings
forth the triangle within, and thus trinity, and the cross which produces
a fifth point. So we have the numbers 3, 4 and 5, and this is the mathematical
expression of the right triangle having 30°, 60° and 90° angles, of which
the legs are 3 and 4, and the hypotenuse 5. It is the only triangle of which
the hypotenuse will be a whole number when the legs are whole numbers too.
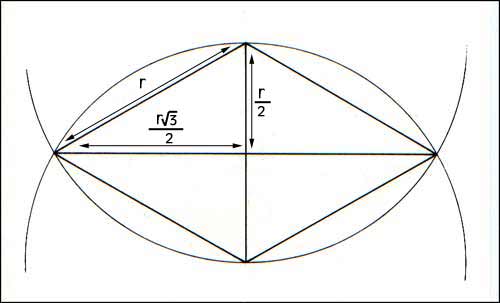
When we call the radius of the circle r, then the following mathematical expressions appear: |
|
Besides the point and the circle, the third geometric structure is the line. And there are three lines of different length. The radius of the circle is r (the vertical axis of the diamond). The distance of the center point of the 'ellipse' or diamond to the circle is r/2. The distance of the same center point to the point where the the two circles cross is (r/2)X√3 (radius divided by two and multiplied by the square root of 3). √3 is the first square root to appear. When measuring the simple distance of the above we obtain (r/2)X√3, or the total length of the long axis of the diamond is rX√3. But when we calculate the relation of the long axis of the diamond to the short axis of the diamond (the cross), we obtain the pure square root of three: rX√3/r = √3.
When we duplicate the circle three more times, we obtain the thirteen points on the circles of which actually ten are attributed to the Sephiroth (sometimes one more for Daath, the 'hidden' Sephiroth). One wonders why they left out the two lower ones.
|
|
Then I asked myself why was the structure drawn in three complete circles with two half circles (top and bottom). It seemed to be part of something else. Let's leave the mathematical expressions behind and return to the two circles: |
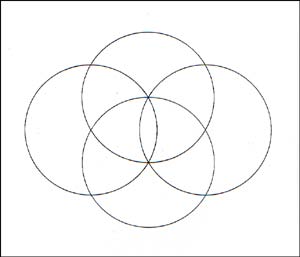 Remember we have four points, two serve as the centers of the two circles, and two on the cross sections of the two circles. Those two cross points seem the be the only likely places that would serve as centers for two more circles: |
|
But this doesn't look quite symmetrical, and the universe likes symmetry, thus it produces two more circles: |
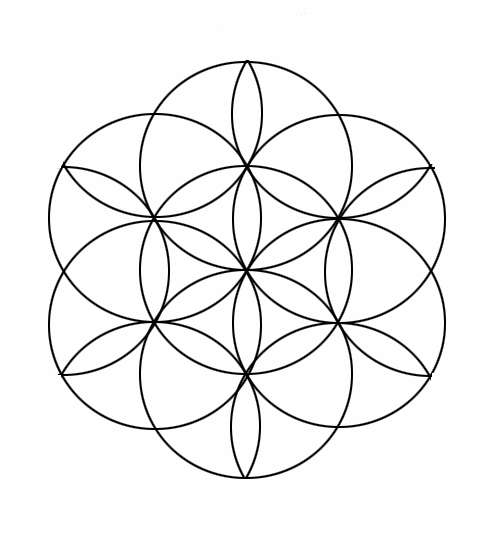
|
Sometimes also depicted as follows when you fill in the remaining 'petals': |
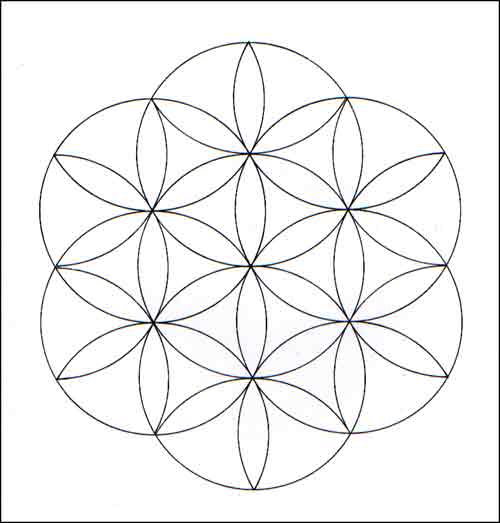
The Tree of Life fits perfectly in here:
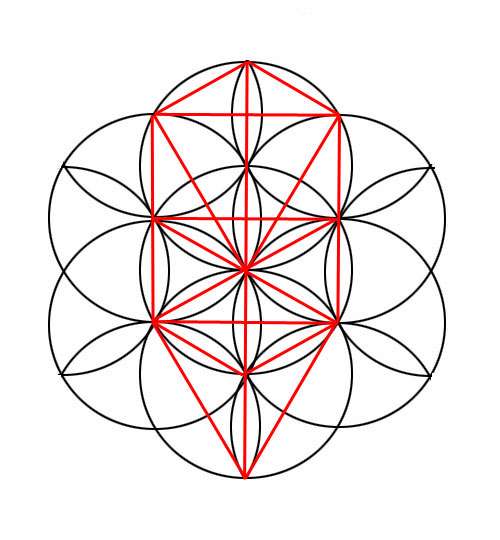
|
Are there more hidden Sephiroth? we will go into this in the following chapters. |